Estudio cualitativo del método de alineación por deriva "Bigourdan"
El método de alineación por deriva "Bigourdan" es muy popular por su sencillez y precisión (si se realiza con las estrellas adecuadas y el tiempo suficiente).
Vamos a estudiar cuál es su fundamento, para ello vamos a definir el sistema ortogonal formado por el eje de rotación de la Tierra (N-S), el eje E-W y el eje que corta al Meridiano del lugar y está contenido en el plano ecuatorial de la Tierra. Así mismo definimos un sistema ortogonal para la montura formado por el eje de AR, el eje de Declinación y el eje del tubo óptico cuando éste se encuentra perpendicular al eje de AR.
Vamos a estudiar cuál es su fundamento, para ello vamos a definir el sistema ortogonal formado por el eje de rotación de la Tierra (N-S), el eje E-W y el eje que corta al Meridiano del lugar y está contenido en el plano ecuatorial de la Tierra. Así mismo definimos un sistema ortogonal para la montura formado por el eje de AR, el eje de Declinación y el eje del tubo óptico cuando éste se encuentra perpendicular al eje de AR.
Cuando nuestra montura ecuatorial no se encuentra correctamente alineada con el polo norte (sur) celeste, matemáticamente decimos que se encuentra "rotada". Esta rotación de la montura hace que tengamos que corregir el eje de azimut, el de elevación, o ambos para conseguir una alineación perfecta. En la figura 2 se puede ver el efecto de una rotación.
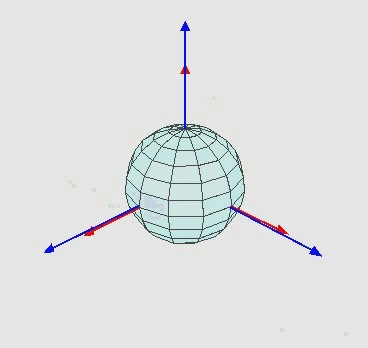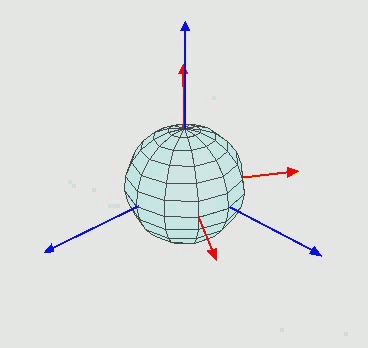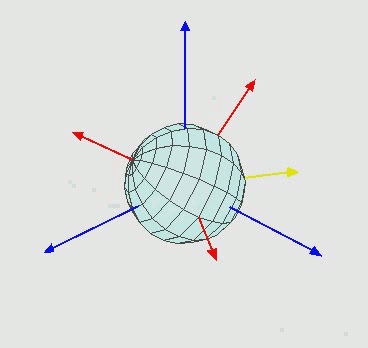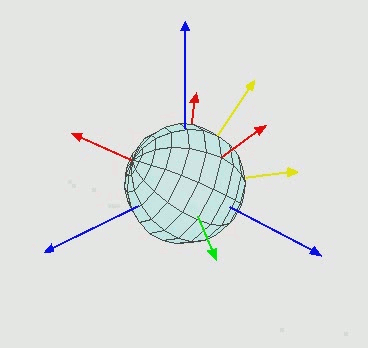
Para corregir la posición de la montura utilizamos dos estrellas, una al sur (norte) y otra al este. Siguiendo el movimiento de la estrella sur (norte) podremos calcular la deriva en azimut de la montura y siguiendo el movimiento de la estrella este podremos calcular la deriva en elevación (ver figura 1).
Para corregir la posición de la montura utilizamos dos estrellas, una al sur (norte) y otra al este. Siguiendo el movimiento de la estrella sur (norte) podremos calcular la deriva en azimut de la montura y siguiendo el movimiento de la estrella este podremos calcular la deriva en elevación (ver figura 1).
Figura 1.
Figura 2.
¿Es posible realizar el método de Bigourdan con una sola estrella?Sin entrar en demasiados detalles matemáticos y sin hacer un desarrollo geométrico completo, vamos a mostrar en qué condiciones se puede realizar una correción de deriva con el método Bigourdan y una sola estrella como el descrito en este artículo. En este caso la corrección de la deriva sólo es posible cuando existe una rotación plana (es decir la deriva se produce sólo en uno de los ejes). Las rotaciones planas se pueden reducir al caso bidimensional (rotaciones en el plano). Un ejemplo de una rotación plana podría ser el mostrado en la figura 1.
Rotaciones en el plano (Consideraciones geométricas)
Sea un vector A en el plano cartesiano definido por sus componentes x e y, descrito vectorialmente a través de sus componentes:
La operación de rotación del punto señalado por este vector alrededor de un eje de giro puede siempre escribirse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector):
RA = A'
En dos dimensiones la matriz de rotación para el vector dado puede escribirse de la manera siguiente:
Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos un nuevo vector A' que ha sido rotado en un ángulo θ en sentido antihorario:
siendo
las componentes del nuevo vector después de la rotación.
Las rotaciones en el plano pueden tratarse igualmente mediantes números complejos, ya que eiα es una rotación de ángulo a.
En resumen, si el punto x = 0, y = 0 es nuestra estrella de referencia, Ax es conocida (espacio de translación debido a la velocidad de la tierra), A'x es el espacio de translación debido a la deriva y (Theta) es el ángulo de deriva (ángulo de giro del plano ecuatorial de la montura respecto al plano ecuatorial celeste). A está contenido en el plano ecuatorial celeste y A' está contenido en el plano ecuatorial de la montura.
Una rotación cónica es una composición de dos rotaciones planas y viene representada por un movimiento como el de la figura 2. El desarrollo matemático anterior no es válido ya que aparece un movimiento en el eje z (desplazamiento Dz).
En el modelo de reducción de la deriva (Bigourdan), cuando ninguno de los ejes de la montura es coincidente con ninguno de los ejes del espacio vectorial x-y-z formado por los vectores 0-N, 0-E y 0-S, para realizar las correciones utilizando la misma estrella habría que realizar correcciones en ambos ejes (0-E y 0-S) con un intervalo de 6h o bien utilizar 2 estrellas situadas sobre meridianos a 90º. Cualquier otra opción no tiene suficiente precisión. por tanto, no es posible aplicar el método con una estrella si uno de los ejes de la montura no es coincidente (meridiano N-S o meridiano N-E).
Demostración del movimiento de rotación y ángulos de Euler.
Método corregido:
Para que el método sea válido, una de las coordenadas astrónomicas de una de las estrellas de referencia debe coincidir aproximadamente con la misma coordenada astronómica de la estrella polar y ambas deben ser coplanarias con el Norte celeste y el centro del sistema de referencia (se encuentran en el mismo meridiano). Ejemplo:
Polaris: AR = 02h 35m 54s
Estrella coplanaria:
Gamma-CANCER = 08h 43mSe encuentran en el mismo meridiano que el Norte celeste (son coplanarias).
Seleccionamos una estrella a 6h de las descritas. Ejemplo:
Estrella de referencia para correción de la deriva:
Epsilon-LEO = 02h 45mLa estrella seleccionada es válida para realizar el método Bigourdan con una sola estrella.
En cualquier caso damos las gracias a Carles por su interesante aportación a la Comunidad de astrónomos aficionados.
Fuentes: Wikipedia
Francisco José Ochando Terreros
NOTAS: Este método se ha corregido para el hemisferio Norte. Puede existir algún error en las coordenadas de los astros. Seguiré perfeccionando la demostración para comprensión de todos.
En el modelo de reducción de la deriva (Bigourdan), cuando ninguno de los ejes de la montura es coincidente con ninguno de los ejes del espacio vectorial x-y-z formado por los vectores 0-N, 0-E y 0-S, para realizar las correciones utilizando la misma estrella habría que realizar correcciones en ambos ejes (0-E y 0-S) con un intervalo de 6h o bien utilizar 2 estrellas situadas sobre meridianos a 90º. Cualquier otra opción no tiene suficiente precisión. por tanto, no es posible aplicar el método con una estrella si uno de los ejes de la montura no es coincidente (meridiano N-S o meridiano N-E).
Demostración del movimiento de rotación y ángulos de Euler.
Método corregido:
Para que el método sea válido, una de las coordenadas astrónomicas de una de las estrellas de referencia debe coincidir aproximadamente con la misma coordenada astronómica de la estrella polar y ambas deben ser coplanarias con el Norte celeste y el centro del sistema de referencia (se encuentran en el mismo meridiano). Ejemplo:
Polaris: AR = 02h 35m 54s
Estrella coplanaria:
Gamma-CANCER = 08h 43mSe encuentran en el mismo meridiano que el Norte celeste (son coplanarias).
Seleccionamos una estrella a 6h de las descritas. Ejemplo:
Estrella de referencia para correción de la deriva:
Epsilon-LEO = 02h 45mLa estrella seleccionada es válida para realizar el método Bigourdan con una sola estrella.
En cualquier caso damos las gracias a Carles por su interesante aportación a la Comunidad de astrónomos aficionados.
Fuentes: Wikipedia
Francisco José Ochando Terreros
NOTAS: Este método se ha corregido para el hemisferio Norte. Puede existir algún error en las coordenadas de los astros. Seguiré perfeccionando la demostración para comprensión de todos.